Introduction
When we are talking about the value of angles most of us are used to think in degree.
In common language the phrase "to do a 180" just sounds better than "to do a 3.141592 radian" or even "to do a PI".
But game-engines, due to their unavoidable background in geometry, are somewhat different.
They use radian instead and that is the standard for almost all areas of mathematics.
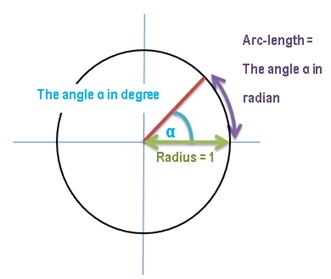
According to Wikipedia, "radian is the ratio between the length of an arc and its radius".
The meaning of this is that on a circle where the radius is 1 unit (the Unit Circle), the angle in radian IS the length of the arc.
The following diagram illustrates this thought.
Pic 1: This picture illustrates the connection between radian and degree. The length of the arc is the angle in radian.
As we all learned at school in times past, the circumference (c) of a circle is ...
So the circumference of a circle with the radius r = 1 (the Unit Circle) would be...
Pic 2: This diagram illustrates the connection of the circumference of the Unit Circle and 2*PI.
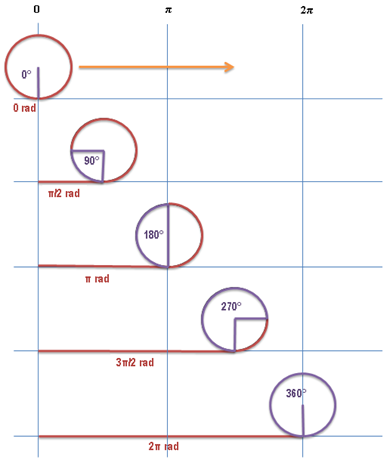
Pretend that the circle unrolls the red line while rolling in the direction of the orange arrow. The purple angle-value has the unit degree (°) the red one's is radian (rad).
Now everybody knows that two PI are 360 degree but in my experience the debugging of such values can be difficult.
So either you calculate the degree-value on the fly within the code or the debug-environment, or you could use the following handy table, that, in most cases, suffices.
Pic 3: We used a 8-direction compass that displays "east" for 0 degree rotation.
For all of you still searching for the right conversion-methods to use within your code:
(Angle in degree) = (Angle in radian) * PI / 180
(Angle in radian) = (Angle in degree) * 180 / PI
In some cases, like when memorizing the rotation within a sprite-class it may be suitable to clamp the value according to its domain since there is no point in memorizing the number of turns in a single direction that brought you to this specific rotation and there always is the problem of a possible value-overflow of a variable.
You don't want to use the method "Clamp" in the XNA-MathHelper - Class because it returns the max-value if the upper boundary is exceeded (and the min-value vice versa).
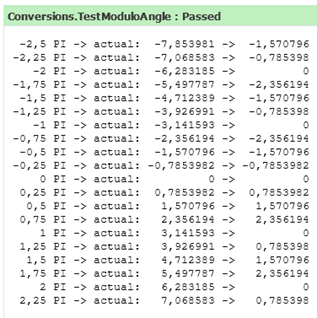
All is good as long as you set the bounds for your valid angle to [-π, +π] as you will get the following output for the calculation: value % MathHelper.Pi
Pic 4: This output shows that a simple modulo-Pi - Calculation is sufficient if you want to constrain your angle to [-π, +π].
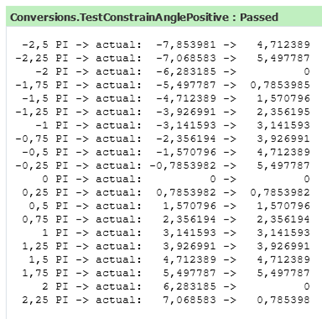
Nevertheless most programmers want the angle to be between zero and 2π, just like this:
Pic 5: The angle constrained to [0, +2π].
Here are two of our methods that we are actually using in production-code.
Pic 6: The first method constrains to a value within -Pi and +Pi by using a simple modulo-operation. The second one does a modulo-operation and always returns a positive value. This takes into account that a quarter-twist in the negative direction is the same as a three-quarter-twist into the positive one.
There are better methods out there using only one modulo-operation instead of two, which is pretty expensive, but we have not yet reached the performance-limits using this one and you know what they say.
Don't solve performance issues that have not yet occurred.
- Wikipedia: http://en.wikipedia.org/wiki/Radian